こんにちは、やっちゃんです。
今日は四分位数を用いた一次元データの外れ値の検出と削除の方法について解説します。
外れ値を確認するまでのやり方は色々なアプローチがあると思いますが、
今回は以下の流れでやっていきます。
①今日は1次元データのヒストグラムを確認して、データの分布を理解し、外れ値もありそうかどうか見る。
②ボックスプロット(箱ひげ図)で実際に外れ値があるかどうかを確定させる
③四分位数から外れ値を算出する
④削除する
用いたデータはKaggleの「Taitanic」です。欠損値ある行は削除しています。
その内の「Fare=客船に乗るために払った金額」を今回用いた一次元データとしました。
|
1 2 3 |
import pandas as pd df = pd.read_csv('titanic.csv') df.head() |

Fareは右から3列目。
それではやっていきます。
データ分布をヒストグラムで確認
データの分布をみて、Fare(料金)はどんな値をとるのか、それぞれの料金を払っている人がどれくらいいるのか(それぞれの金額の頻出度)をみます。
ヒストグラムでまず初めに1次元データの様子を理解はすること、散布図で2次元データの様子を理解することは非常に大事ですので、データ解析の際は欠損値の前処理前後で最初にみる癖をつけましょう。
|
1 |
df.hist("Fare") |
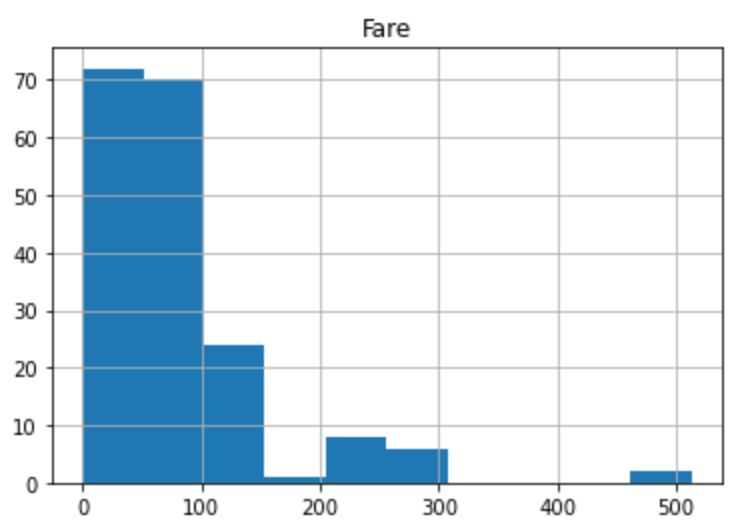
右に裾が長いデータとなってます。料金は0~100範囲で支払いをしている人が多いようです。
500前後支払うVIPな金持ちたちも数人いるみたいですね。しかし、本当にごく少数ですので、外れ値な可能性があります。ボックスプロットで確認していきましょう。
ボックスプロットで外れ値があるか明確にする
ボックスプロットを下に示しました。
外れ値は大まかに言えば、上ひげより上に分布する値と下ひげより下に分布する値は外れ値と思ってください(厳密には違うので計算で出します)。
|
1 |
df.boxplot(column='Fare', figsize=(5,5)) |
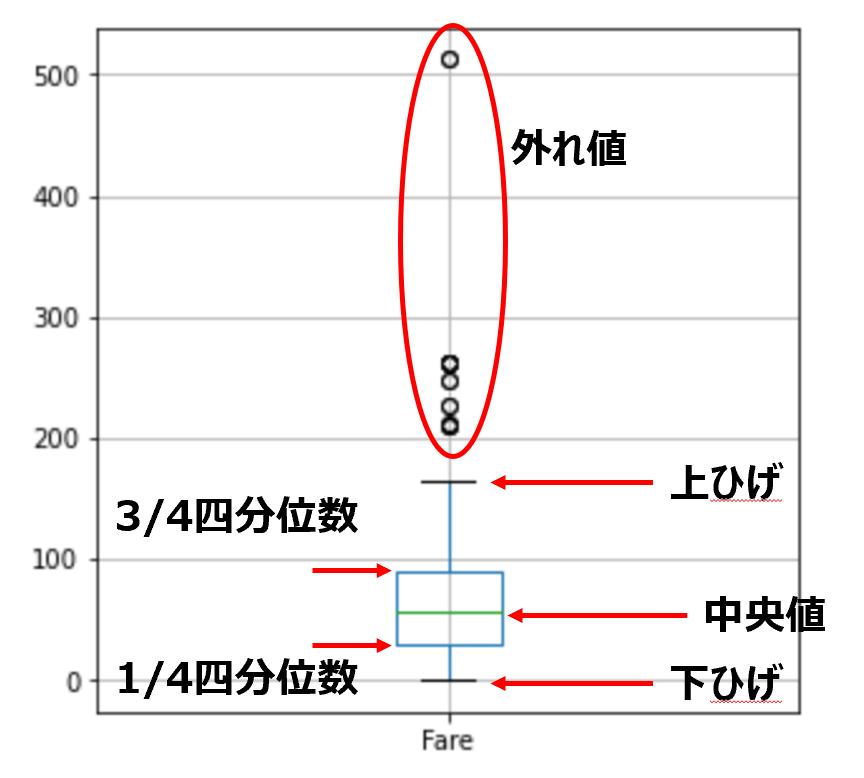
今回は下ひげより下に分布された値はありませんでした。
ですので、赤丸で囲った部分のみが外れ値です。
四分位数から外れ値を算出
それでは正確な外れ値の算出方法を説明します。
上ひげより大きな値をとる正確な外れ値は以下の計算式を用いて算出します。
3/4四分位数+1.5×(3/4四分位数‐1/4四分位数)より外側(=大きい値)です。
3/4四分位数+1.5×(3/4四分位数‐1/4四分位数)をupper_outliersと名付けたときの
Pythonコードが下記です。
|
1 2 3 4 |
q1= df["Fare"].quantile(0.25)#1/4四分位数 q2= df["Fare"].quantile(0.75)#3/4四分位数 upper_outliers = q2+1.5*(q2-q1)#四分位範囲 upper_outliers |
upper_outliers = 180.45 となりました。
3/4四分位数+1.5×(3/4四分位数‐1/4四分位数)より大きな値が外れ値となるので、
180.45より大きな値が外れ値となります。
また、今回は下側の外れ値はボックスプロットでないことを確認したので、
正確な外れ値の範囲を算出する必要はありませんでしたが、
ボックスプロットで下ひげより小さな値が多数見られたときは
計算式「1/4四分位数-1.5×(3/4四分位数‐1/4四分位数)」で算出した値より
小さな値が外れ値です。
1/4四分位数-1.5×(3/4四分位数‐1/4四分位数)をlower_outliersと名付けます。
|
1 2 3 4 |
q1= df["Fare"].quantile(0.25)#1/4四分位数 q2= df["Fare"].quantile(0.75)#3/4四分位数 lower_outliers = q1-1.5*(q2-q1)#四分位範囲 lower_outliers |
これで算出した値より小さな値が外れ値ですので、覚えておきましょう。
外れ値の削除
df = df[(df[“Fare”] < 180.45)]で料金が180.45より小さい値だけを抽出します。
(=180.45より大きな値は削除)
そして前後の行数のdf.shapeで確認し、
どれくらいのサンプル(お客さんデータ)が外れたのかも確認しましょう。
|
1 2 3 |
print('before', df.shape) df = df[(df["Fare"] < 180.45)] print('after', df.shape) |
before (183, 12)
after (167, 12)
つまり、もともと183行(183人の顧客データ)でしたが、外れ値を含む行数を削除することで、
顧客データは167人となりました。
下側の外れ値がある場合も同じようにして処理しましょう(符号の向きに気を付けて)。
終わりに(仕事提案に向けた外れ値の扱いについて)
外れ値ありきでデータ解析するのが都合がよい時、
外れ値は削除してデータ解析するのが都合がよい時、
そのどちらも存在します。
ですので、外れ値=削除するべきものと考えるとは安直すぎるので注意してください。
Case by Caseで対応しましょう。
また、何らかの変数に外れ値があるということは、その外れ値に該当する顧客データは
ある特異的な顧客である可能性、その人たち特有の悩みを持っている顧客である可能性、
ある特有の感性をもっている顧客である可能性など、様々な可能性があります。
つまりニッチな領域とうことです。ブルーオーシャンの可能性がある領域ということです。
あらたなサービス、商品開発につながる原石である可能性があります。
外れ値だ!いらない!削除!
ではなく。
外れ値だ!特異的だ!ニッチだ!新たな開発プロジェクト提案したるぜい!!
という風なプラスな考え方で考えることが大事だと思います。
それでは今日はここで終わりにします^^。
最後まで読んでくださりありがとうございました!



コメント