みなさん、こんにちは。やっちゃんです。
教師なし学習の一つである主成分分析(PCA)について、原理から評価方法まで説明します。Pythonコードも載せていくのでご参考いただけたら幸いです^^。
主成分分析:多変量データをもとに変数間あるいはサンプル間の類似性を評価するときに使います。次元圧縮法の1つです。
【使い道】仕事に直結させる方法として、マーケッターは市場調査で使うのが一般的でしょうか?例えば世に存在するあらゆるブランドのコーヒーの味や匂いを官能評価をして様々な評価項目の結果から各ブランドをいくつかにグループに分けられたとします。そこからコーヒーブランドの割り振りがすくなかったグループを探索して、ブルーオーシャンの味や香りのコーヒー開発に役立てます。また、ブランドイメージを消費者へのアンケート項目にして、斬新なコンセプトの新ブランドをたちあげるなどなど。使い道は色々あると思います。
今回はKaggleに掲載されているIris(アヤメ:花の名前)データを使います。IrisにはSetosa、Verginica、versicolorの3種類が存在します。これらをがく片の長さと幅、花びらの長さと幅の4つの特徴から分類できるか主成分分析でみていきましょう。
*注意点:主成分分析はデータに欠損値があるときは使えません。その際は欠損値がある行は削除するか、欠損値をなんとか補完するか、主成分分析ではなく多次元尺度構成法(MDS:次元圧縮法の一つ)をつかいましょう。
それではやっていきましょう!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import pandas as pd # データを扱うための標準的なライブラリ import numpy as np # 多次元配列を扱う数値演算ライブラリ from sklearn.decomposition import PCA,TruncatedSVD #主成分分析ライブラリ import matplotlib.pyplot as plt # グラフを描画するライブラリ import seaborn as sns %matplotlib inline # jupyter内に描画 df = pd.read_csv("Iris.csv")#, index_col=5) df = df.drop(["Id"], axis=1) df.head() |
|
1 |
df.info() |
|
1 |
df["Species"].value_counts() |

標準化しましょう。単位が違う対象でも比べられるようになります。今回で言えば、アヤメのがく片の長さはcmで幅もcm、花びらも同様ですので、必ずしも標準化する必要はないですが、基本標準化したほうが経験上分類精度がよくなります。毎回、標準する時しない時で分類精度を比べてみるのがベストです。
|
1 2 3 4 |
#標準化 dfs = df.iloc[:, 0:].apply(lambda x: (x-x.mean())/x.std(), axis=0) dfs = dfs.drop(["Species"], axis=1) dfs.head() |
|
1 2 3 4 5 6 7 |
#主成分分析の実行 pca = PCA() pca.fit(dfs) # データを主成分空間に写像 feature = pca.transform(dfs) # 主成分得点 pd.DataFrame(feature, columns=["PC{}".format(x + 1) for x in range(len(dfs.columns))]).head() |
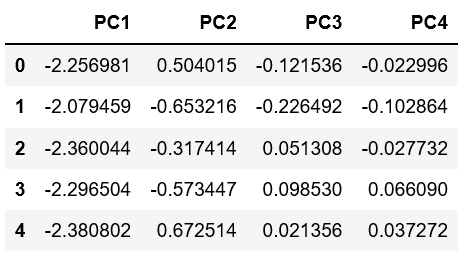
データ行列をもとに、サンプルの分散が最大となる軸を主成分第1軸、主成分第1軸に直交して分散が大きな軸を第2軸と軸を求めていき、順々に主成分軸を求めます。そして分散の大きな軸の上にサンプルをプロットします。それが主成分プロットです。
|
1 2 3 4 5 6 7 8 9 10 |
# 第一主成分と第二主成分でプロットする plt.figure(figsize=(6, 6)) plt.scatter(feature[0:49, 0], feature[0:49, 1], c="b", alpha=0.5, label="setosa") plt.scatter(feature[50:99, 0], feature[50:99, 1], c="r", alpha=0.5, label="virginica") plt.scatter(feature[100:149, 0], feature[100:149, 1], c="g", alpha=0.5, label="versicolor") plt.legend() #loc="upper left", fontsize=10 plt.grid() plt.xlabel("PC1") plt.ylabel("PC2") plt.show() |
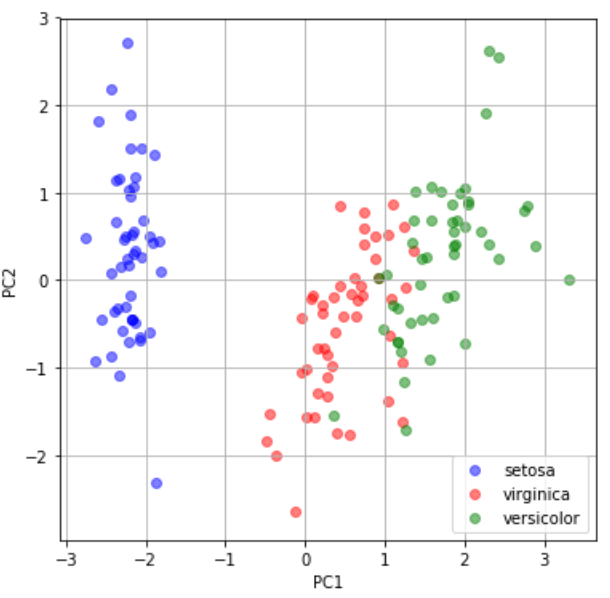
3つのアヤメの品種がしっかり分類できているのがわかります。特にsetosa(青丸)は他2つよりもよく分類されていることがわかります。比べてvirginicaとversicolorは重なっていて主成分分析で分類するのは難しい部分もあるよう。
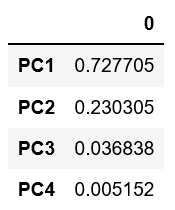
それでは寄与率と累積寄与率を算出して分類の精度を評価していきましょう。寄与率とは全分散に対すて着目した主成分の分散値です(よくわからない方。統計知識は難しいですが、別途べつの記事で解説しますね。結果の解釈だけでも理解できればOK!)。
|
1 2 |
# 寄与率 pd.DataFrame(pca.explained_variance_ratio_, index=["PC{}".format(x + 1) for x in range(len(dfs.columns))]) |
|
1 2 3 4 5 6 7 8 |
# 累積寄与率を図示する import matplotlib.ticker as ticker plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True)) plt.plot([0] + list( np.cumsum(pca.explained_variance_ratio_)), "-o") plt.xlabel("Number of principal components") plt.ylabel("Cumulative contribution rate") plt.grid() plt.show() |
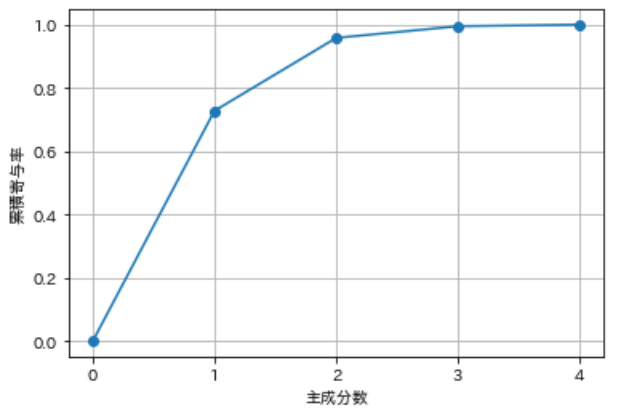
第2主成分までの累積寄与率で9割超えてますね。抜群にいい評価です。人によって解釈は違うかもしれませんが、私は第2主成分までで60%、第3主成分までで70~80%超えていれば悪くはないって感じで評価してます。
最後に因子負荷量の作図をして、主成分プロットの解釈をしていきましょう。因子負荷量とはある変数とある主成分軸の相関のことです。
|
1 2 3 4 5 6 7 8 9 |
#因子分析 plt.figure(figsize=(6, 6)) for x, y, name in zip(pca.components_[0], pca.components_[1], dfs.columns[0:]): plt.text(x, y, name) plt.scatter(pca.components_[0], pca.components_[1], alpha=0.8) plt.grid() plt.xlabel("PC1") plt.ylabel("PC2") plt.show() |
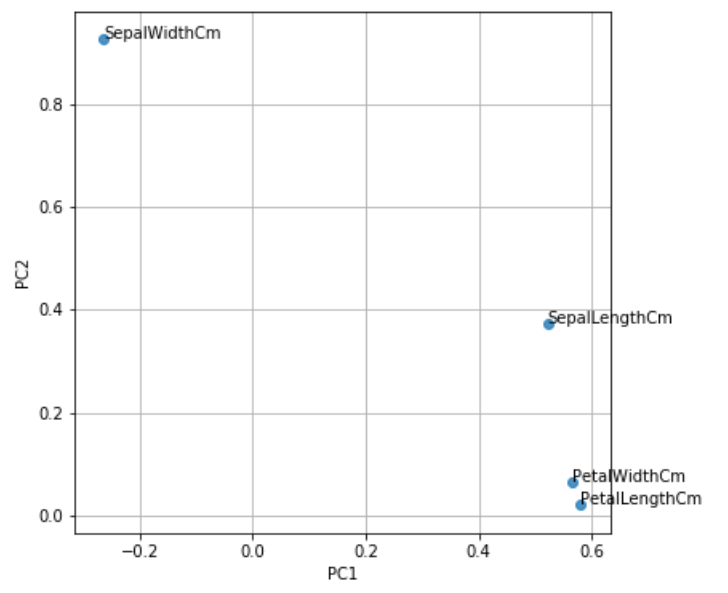
さきほど、setosaはPC1<0に集まって分類されていましたよね。ではsetosaを分類する上で重要だった因子はなんでしょうか?この因子散布図をみれば一目瞭然です。一番左上にあるSepalWidthがPC1<0に分布されているのでsetosaの一番の特徴であることがわかります。
【最後に】
いかがだったでしょうか。主成分分析の基本はこれで大体OKです。結果の解釈の仕方も理解していただけたかと思います。学術的な研究活動、企業での研究活動、マーケッターとしての市場調査、新ブランドコンセプト立案など様々な面で使える手法ですので、ぜひマスターしてみてください。
今回は第1主成分と第2主成分のみでプロットし、結果の解釈を行っていきました。しかし、実際にアンケート調査等で市場調査する場合は第3主成分のプロットまでみてみるといいです。先述のグラフをPC1×PC2だけでなく、PC1×PC3やPC2×PC3まで調べてみると、新たな戦略や戦術立案にむけた財宝が眠ってるかもしれません。
ご質問、ご意見がある際には是非ご教授いただきたく思います。
最後まで読んでくださってありがとうございました^^!。


コメント