みなさんこんちには、やっちゃんです。
本日はこれまでも紹介してきた多変量解析の一種である次元圧縮法についてです。次元圧縮法には主成分分析(PCA)、多次元尺度構成法(MDS)、t-SNE法などがありますが、PCA以外のコード紹介やPCAとの違いについては語ってきませんでした。簡単にご紹介させていただきます。
まず次元圧縮法は、多次元(多変数)のデータを情報をできるだけ除外せずに低次元に削減する方法する方法(2次元にすることが多い)です。データを可視化したい時は本当に使えますね。それではPCAとMDS、t-SNEはどのようにちがうのでしょうか。
主成分分析(PCA)は線形手法であり、解釈性が高く、一意に決まることが特徴となります。データの分散が最大となる軸を主成分第1軸、主成分第1軸に直交して分散が大きな軸を第2軸と軸を求めていき、順々に主成分軸を求めて、多次元を低次元に縮約していきます。
MDSとt-SNEは非線形手法です。PythonやRコード内で変更できる乱数やパラメータ等により結果が変化します。
t-SNEは元のデータ同士の距離が正規分布に従うと仮定した時に、次元削減済みのデータ毎の距離がt分布に従うように配置します。t分布は正規分布よりも裾が広い分布となるので近いデータはより近くに、遠いデータはより遠くに配置されるようになります。
MDSはデータ同士の距離の情報から、その距離を維持するように低次元委プロットする手法です。距離情報をもとに地図を作る感じです。
経験上、t-SNE、MDSともにPCAよりもデータの分離性が高くなることが多いです。PCAで新しい特徴量を回帰モデルや分類モデルをつくる際に説明変数として加えるとモデル性能が良くなる場合が多いですが、t-SNEやMDSも同様です。
実際にIris(3品種のアヤメ)データ(from Kaggleで見てみましょう。)
PCAでのIrisデータの可視化は過去にも行いましたのでPythonコードは過去の記事をご参考ください。今回は可視化結果のみ載せます。
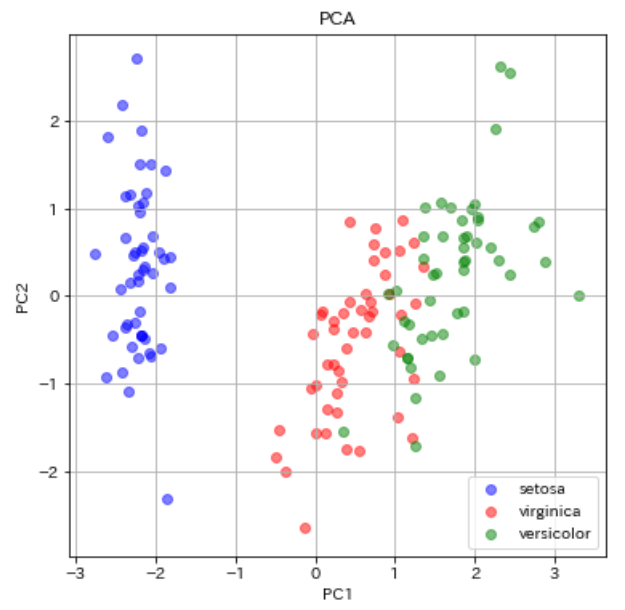
続いてMDSでの可視化です。
|
1 2 3 4 5 6 7 8 9 10 11 |
from sklearn import manifold #MDSのライブラリimport clf = manifold.MDS(n_components=2, n_init=1, max_iter=100,random_state=0)#分離結果を左右する乱数とハイパーパラメータ X_mds = clf.fit_transform(dfs) plt.figure(figsize=(6, 6)) plt.scatter(X_mds[0:49, 0], X_mds[0:49, 1], c="b", alpha=0.5, label="setosa") plt.scatter(X_mds[50:99, 0], X_mds[50:99, 1], c="r", alpha=0.5, label="virginica") plt.scatter(X_mds[100:149, 0], X_mds[100:149, 1], c="g", alpha=0.5, label="versicolor") plt.legend() plt.title("MDS") plt.grid() plt.show() |
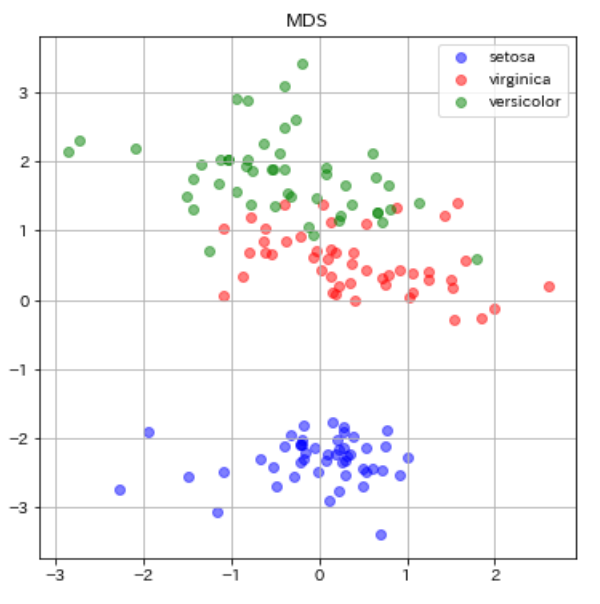
続いてt-SNEです。
|
1 2 3 4 5 6 7 8 9 10 |
from sklearn.manifold import TSNE #ライブラリimport transformed = TSNE(n_components=2,perplexity=60, random_state=0).fit_transform(dfs) #可視化結果を左右するパラメータ plt.figure(figsize=(6, 6)) plt.scatter(transformed[0:49, 0], transformed[0:49, 1], c="b", alpha=0.5, label="setosa") plt.scatter(transformed[50:99, 0], transformed[50:99, 1], c="r", alpha=0.5, label="virginica") plt.scatter(transformed[100:149, 0], transformed[100:149, 1], c="g", alpha=0.5, label="versicolor") plt.legend() plt.title("TSNE") plt.grid() plt.show() |
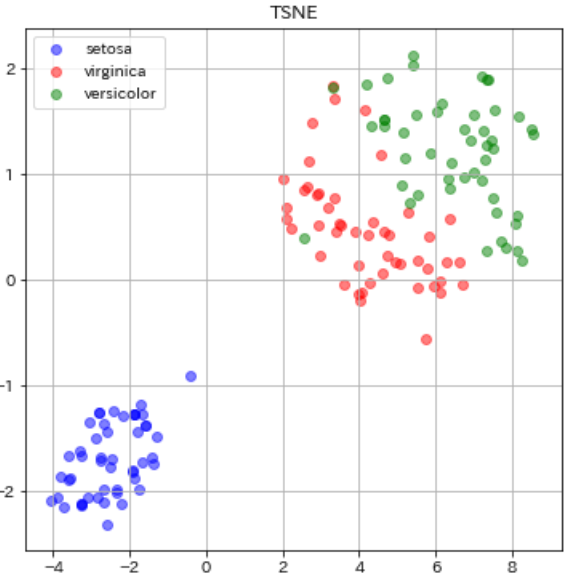
今回のPCAとMDSの比較では、あまりMDSの分離性は向上しませんでした。青丸のsetosa同士のデータが近い部分に分布してくれたくらいでしょうか。他2つにおいては同じ品種のデータ同士の散らばりも似たような感じですし、virginica(赤)とversicolor(緑)の重なっている部分の改善も見られませんでしたね(分離してくれなかった)。
ではt-SNEはどうでしょうか。PCAやMDSに比べて、全体的に同じ品種のデータ間の分布が近くなっているのがわかると思います。これはt-SNEの特徴であるt分布のおかげですね。t-分布は正規分布に比べて裾が長い分布となっているので、近しいデータはより近くに、遠いデータはより遠くに配置されるようになっています(PCAの可視化図と比べてみてください)。そのおかげで、完璧とまでは言えませんが、virginica(赤)とversicolor(緑)の重なりも改善し、より分離がてきている結果となりました。
本日は以上となります。それぞれの次元圧縮法を試してみて、一番分離が良かった時の手法で得られた新たな特徴量を回帰式や分類モデルを作るときの説明変数に加えてみてください。性能が良いモデルがきっと作れると思いますよ♪
最後まで読んでくださってありがとうございました^^。


コメント